HUKUM KEKEKALAN MOMENTUM

HUKUM KEKEKALAN MOMENTUM

Hukum Kekekalan Momentum
Tidak peduli berapapun massa dan kecepatan benda yang saling bertumbukan, ternyata momentum total sebelum tumbukan = momentum total setelah tumbukan. Hal ini berlaku apabila tidak ada gaya luar alias gaya eksternal total yang bekerja pada benda yang bertumbukan. Jadi analisis kita hanya terbatas pada dua benda yang bertumbukan, tanpa ada pengaruh dari gaya luar.

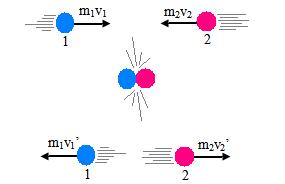
Jika dua benda yang bertumbukan diilustrasikan dengan gambar di atas, maka secara matematis, hukum kekekalan momentum dinyatakan dengan persamaan :

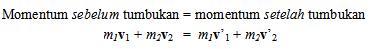
m₁ = massa benda 1,
m₂ = massa benda 2,
v₁ = kecepatan benda 1 sebelum tumbukan,
v₂ = kecepatan benda 2 sebelum tumbukan,
v’₁ = kecepatan benda 1 setelah tumbukan,
v’₂ = kecepatan benda 2 setelah tumbukan.
Jika dinyatakan dalam momentum, maka :
m₁v₁ = momentum benda 1 sebelum tumbukan, m₂v₂ = momentum benda 2 sebelum tumbukan, m₁v‘₁ = momentum benda 1 setelah tumbukan, m₂v‘₂ = momentum benda 2 setelah tumbukan
Kita tulis kembali persamaan hukum II Newton :

Ketika bola 1 dan bola 2 bertumbukan, bola 1 memberikan gaya pada bola 2 sebesar F₂₁, di mana arah gaya tersebut ke kanan (perhatikan gambar di bawah)

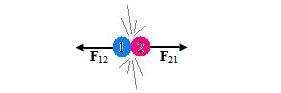
Momentum bola 2 dinyatakan dengan persamaan :

Berdasarkan Hukum III Newton (Hukum aksi-reaksi), bola 2 memberikan gaya reaksi pada bola 1, di mana besar F₁₂ = – F₂₁. (Ingat ya, besar gaya reaksi = gaya aksi. Tanda negatif menunjukan bahwa arah gaya reaksi berlawanan dengan arah gaya aksi)
Momentum bola 1 dinyatakan dengan persamaan :

Jenis- Jenis Tumbukan

Berdasarkan berlaku atau tidaknya hukum kekekalan energi mekanik (khususnya energi mekanik), tumbukan terbagi atas dua jenis, yaitu Tumbukan Lenting Sempurna dan Tumbukan tidak Lenting. Tumbukan Lenting Sempurna jika pada peristiwa tumbukan itu energi kinetik system adalah tetap. Tumbukan Tidak Lenting jika pada peristiwa tumbukan itu terjadi pengurangan energi kinetik system. Tumbukan tidak lenting disebut tidak lenting sama sekali jika sesaat sesudah tumbukan, kedua benda saling menempel dan keduanya bergerak bersama dengan kecepatan yang sama.

1. Tumbukan Lenting Sempurna

Jenis tumbukan di mana berlaku kekekalan momentum dan kekekalan energi kinetic disebut Tumbukan Lenting Sempurna. Hukum kekekalan momentum memberikan.

m1v1 + m2v2 = m1v1’ + m2v2’

Untuk tumbukan lenting sempurna berlaku hokum kekekalan energi kinetic, yaitu energi kinetic system sasaat sebalum dan sesudah tumbukan sama besar.

EK1 + EK2 = EK1’ +EK2’

½ m1v12 + ½ m2v22 = ½ m1(v1’)2 + ½ m2(v2’)2

Untuk tumbukan lenting sempurna, kecepatan relative sesaat sesudah tumbukan sama dengan minus kecepatan relative sesaat sesudah tumbukan.

2. Tumbukan Tidak Lenting Sama Sekali


Pada jenis tumbukan tidak lenting sama sekali, sesaat setelah tumbukan kedua benda bersatu dan bergerak bersamadengan kecepatan yang sama. Contohnya khas dari tumbukan tidak lentung sama sekali adalah pada ayunan balistik di mana peluru tertanam dalam balok sasaran, dan keduanya kemudian mengalamisuatu gerak ayunan.

Karena pada tumbukan tak lenting sama sekali kedua benda bersatu setelah tumbukan, berlaku hubungan kecepatansesudah tumbukan sebagai berikut.

v2’ = v1’ = v

Demi mempersingkat penyelesaiannya, kita dapat menggabungkan keduanya untuk mendapatkan persamaan sebagai berikut.

m1v1 + m2v2 = m1v1’ + m2v2’

m1v1 + m2v2 = (m1+m2)’

Tumbukan Lenting Sebagian
v2 - v1 adalah kecepatan relatif benda pertama terhadap benda kedua sebelum benda itu bertumbukan. v2` - v1` adalah kecepatan relatif benda pertama terhadap benda kedua setelah benda itu bertumbukan. Pada kebanyakan tumbukan, besar kecepatan relatif itu tidak tetap, melainkan berkurang dengan suatu faktor tertentu yang disebut koefisien restitusi (e).    misalkan sebuah bola dijatuhkan ke lantai, bola = benda 1 dan lantai = benda 2, maka sebelum dan sesudah tumbukan kecepatan lantai = 0 sehingga : e = - v2` / v2   Umpamanya tinggi benda ketika dijatuhkan adalah h1, dan benda memantul setinggi h2 dari lantai. Dengan menggunakan persamaan gerak jatuh bebas kecepatan benda ketika mengenai lantai dan kecepatan memantulnya dapat dinyatakan dengan h1, h2, maka :   dan   maka diperoleh nilai e:   h1 = tinggi benda saat dijatuhkan (m) h2 = tinggi benda saat memantul kembali (m)

3. Koefisien Restitusi untuk Tumbukan Satu Dimensi

Tumbukan lenting sempurna dan tumbukan tak lenting sama sekali adalah dua kasus yang ekstrem. Pada umumnya sebagian besar tumbukan berada di antara kedua ekstrem itu. Tumbukan itu disebut tumbukan lenting sebagian.

Koefisien restitusi adalah negative perbandingan antara kecepatan relative sesaat sesudah tumbukan dengan kecepatan relative sesaat sebelum tumbukan untuk tumbukan satu dimensi.

e = -∆v’ / ∆v = -(v’2 – v’1) / v2 - v1